在前一篇文章發現了，在某些場景下合成的結果表現並不是很好。

像是這張圖這樣，可以看到雖然演算法找尋的邏輯都相同但是整體畫面就是不和諧！
因此接下來嘗試另外一種演算法，針對消失點的演算法！

簡單來說呢！每個物體都會有一個消失點，因此我們要平行的不會是該物體的斜率而是將海報的上下邊之消失點移至與物品相同，進而使之真的融入場景中！示意圖如下：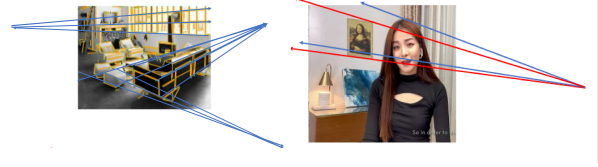

首先一樣將想法拆成 to-do list 整理：
-［　］根據水平射線找尋適合的線
-［　］根據適合的線進行消失點調整

在這邊希望可以找到最能代表場景的兩條線，也就是牆壁或是大型家具的線，這兩條線會成為視線的參考線。

在找出最長線條前會需要先計算長度。

def line_length(line):
        return np.linalg.norm(line[1] - line[0])

接下來就來找出最長的兩條線吧！

# Compute the lengths of each line
line_lengths = [(line, line_length(line)) for line in h_line]

# Sort the lines by length in descending order
sorted_lines = sorted(line_lengths, key=lambda x: x[1], reverse=True)

# Get the two longest lines
longest_lines = sorted_lines[:2]

這邊最主要的邏輯就是先算出線的長度，接著進行排序，排序完成後取前兩個即可！
-［✅］根據水平射線找尋適合的線
-［　］根據適合的線進行消失點調整
再來下一個任務是根據適合的線進行消失點調整，這邊就是這次變更演算法不同的地方。

def calculate_vanishing_point(line1, line2):
    # 從每條線中提取兩個點
    x1, y1 = line1[0]
    x2, y2 = line1[1]
    x3, y3 = line2[0]
    x4, y4 = line2[1]
    
    # 計算線的斜率和 y 截距
    m1 = (y2 - y1) / (x2 - x1) if x2 != x1 else float('inf')
    b1 = y1 - m1 * x1 if m1 != float('inf') else None
    
    m2 = (y4 - y3) / (x4 - x3) if x4 != x3 else float('inf')
    b2 = y3 - m2 * x3 if m2 != float('inf') else None
    
    # 處理平行線的情況
    if m1 == m2:
        return None  # 平行線沒有交點
    
    # 計算交點
    if m1 == float('inf'):
        x = x1
        y = m2 * x + b2
    elif m2 == float('inf'):
        x = x3
        y = m1 * x + b1
    else:
        x = (b2 - b1) / (m1 - m2)
        y = m1 * x + b1
    
    return (x, y)

這個函數 calculate_vanishing_point 用來計算兩條線的交點（如果有）。它會透過計算兩條線的斜率與截距，進而找到交點。如果兩條線平行，則返回 None，因為它們沒有交點。

函數的第一步是從每條線中提取兩個點的座標。每條線由兩個點表示，第一條線的兩個點為 (x1, y1) 和 (x2, y2)，而第二條線的兩個點為 (x3, y3) 和 (x4, y4)。這些點將被用來計算每條線的斜率和截距。

接下來，根據這些座標來計算每條線的斜率和截距。斜率的計算公式為 (y2 - y1) / (x2 - x1)，如果兩個 x 座標相同，則該線為垂直線，斜率被設為無限大 float('inf')。如果斜率是無限大，那麼這條垂直線的截距不適用，設為 None。否則，計算 y 截距，公式為 b = y1 - m * x1。

接著，函數會檢查這兩條線是否平行。如果它們的斜率相同，這表示它們平行且不會相交，因此返回 None。

如果兩條線不平行，函數則會計算它們的交點。若其中一條線是垂直線，則交點的 x 值將是該垂直線的 x 座標，而 y 值則是另一條線根據其方程計算得出。如果兩條線都不是垂直線，則聯立兩條線的方程，通過斜率和截距來計算交點的 x 和 y 座標。

函數最終返回這兩條線的交點 (x, y)，如果沒有交點則返回 None。
最終取得消失點後就可以來進行線段調整了！

def adjust_vanishing_point(line1, line2, new_vanishing_point):
    # 計算線段的方向向量
    dir1 = np.array(line1[1]) - np.array(line1[0])
    dir2 = np.array(line2[1]) - np.array(line2[0])
    
    # 計算新的方向向量
    new_dir1 = np.array(new_vanishing_point) - np.array(line1[0])
    new_dir2 = np.array(new_vanishing_point) - np.array(line2[0])
    
    # 計算縮放因子
    scale1 = np.linalg.norm(dir1) / np.linalg.norm(new_dir1)
    scale2 = np.linalg.norm(dir2) / np.linalg.norm(new_dir2)
    
    # 計算新的終點
    new_end1 = np.array(line1[0]) + new_dir1 * scale1
    new_end2 = np.array(line2[0]) + new_dir2 * scale2
    
    # 返回新的線段
    return [line1[0], new_end1.tolist()], [line2[0], new_end2.tolist()]

目的

調整兩條線段，使它們的交點（消失點）移動到指定的新位置，同時保持線段的起點不變和長度比例不變。

參數

• line1： 第一條線段，格式為 [(x1, y1), (x2, y2)]
• line2： 第二條線段，格式為 [(x3, y3), (x4, y4)]
• new_vanishing_point： 新的消失點坐標 (x, y)

實現步驟

1. 計算原始方向向量

   • dir1 = line1[1] - line1[0]：第一條線段的方向向量
   • dir2 = line2[1] - line2[0]：第二條線段的方向向量

2. 計算新的方向向量

   • new_dir1 = new_vanishing_point - line1[0]：從第一條線段起點到新消失點的向量
   • new_dir2 = new_vanishing_point - line2[0]：從第二條線段起點到新消失點的向量

3. 計算縮放因子

   • scale1 = ||dir1|| / ||new_dir1||：保持第一條線段長度不變的縮放因子
   • scale2 = ||dir2|| / ||new_dir2||：保持第二條線段長度不變的縮放因子

4. 計算新的終點

   • new_end1 = line1[0] + new_dir1 * scale1：第一條線段的新終點
   • new_end2 = line2[0] + new_dir2 * scale2：第二條線段的新終點

5. 返回新的線段

   • 返回格式：[line1[0], new_end1], [line2[0], new_end2]

返回新的線段後即可調整圖像！最後我們來看看結果吧！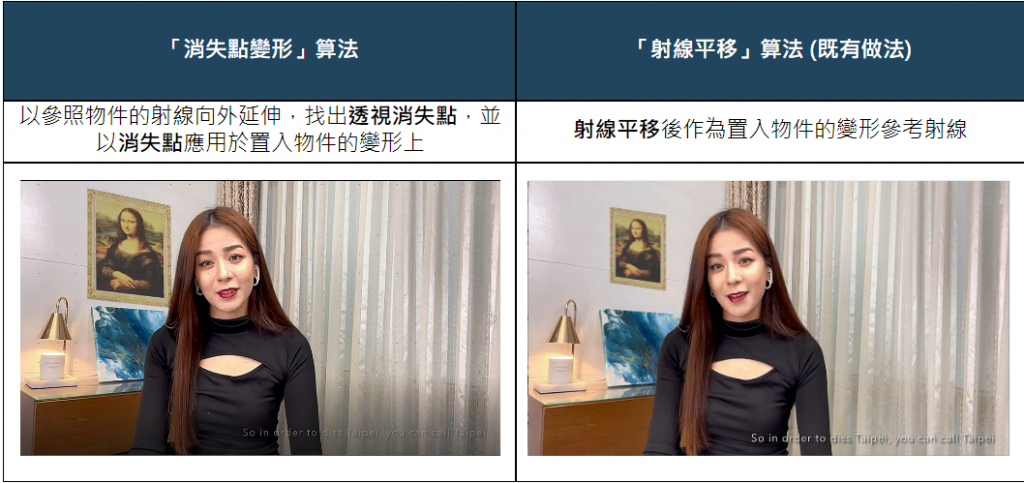


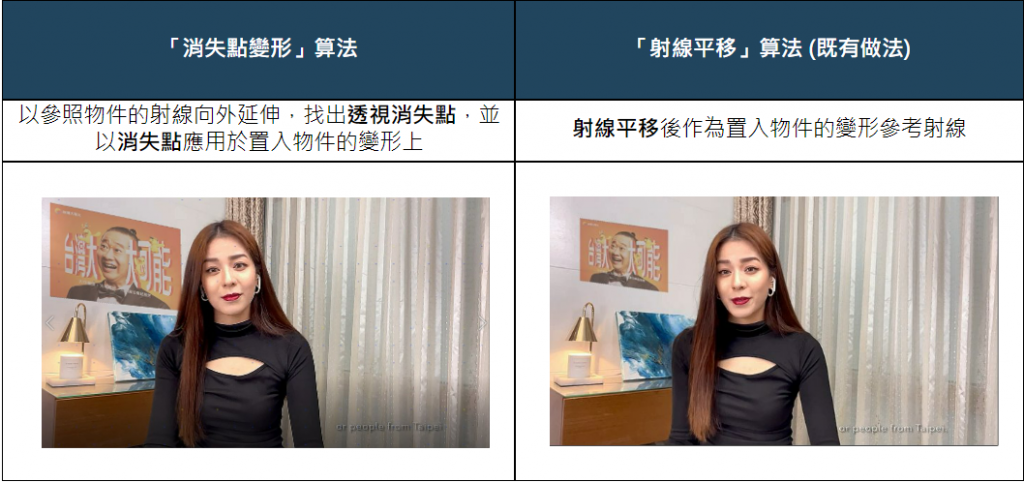
可以看到相較於射線平移，消失點變形會更自然一點，但更重要的是此算法的應用範圍更廣！

如有任何問題歡迎在下方留言提問！

撰文者: RenHe Huang